
지난번에는 2개 집단 간의 평균의 차이를 검정하는 독립표본t-검정을 진행했다. 그렇다면, 3개 이상 집단의 평균 차이를 검정하고 싶을 때는 어떻게 해야 할까? 알다시피 성별이라는 변수는 ① 남성 ② 여성으로 구분된다. 성별에 따른 평균의 차이를 보고싶을 때에는 독립표본t-검정을 하면 된다. 반면, 학급이라는 변수가 있다면 이는 ① 새싹반, ② 별빛반, ③ 푸른반, ④ 초록반 등의 세 개 이상 범주로 구분될 수 있다. 이러한 학급들 간의 평균 만족도를 보고 싶다면 일원배치분산분석(one-way ANOVA)을 적극 활용해 볼 수 있다.
오늘 사용한 예제 파일은 ‘hourlywagedata.sav’이다. 이름에서도 알 수 있듯, 시간당 임금(받는 급여)을 표시한 데이터라고 보면 된다.
파일을 열어보면 심플하게 세 개의 변수로 구성된 것을 알 수 있다. 먼저 [agecat]은 연령 범주를 나타내는 것으로 ‘1=18~30세’, ‘2=31~45세’, ‘3=46~65세’로 코딩되어 있다. [agecat]은 세 개의 범주로 구성되어 있으므로 일원배치분산분석(one-way ANOVA)을 할 수 있는 조건을 갖추었다(범주가 3개 이상일 때 사용므로). [yrs]는 근속 연수를 나타내는 변수로 ‘1=5년 이하 근무’, ‘2=6~10년 근무’, ‘3=11~15년 근무’, ‘4=16~20년 근무’, ‘5=21~35년 근무’, ‘6=36년 이상 근무’로 해석하면 된다. 마지막으로 [wage]는 근로자가 받는 시간당 급여이다. [agecat]과 [yrs]는 3개 이상의 집단으로 구성된 명목척도이며, [wage]는 연속형 자료로 구성된 비율척도라는 것을 기억하고 다음으로 넘어가자.
- [agecat] : 1=18~30세, 2=31~45세, 3=46~65세
- [yrs] : 1=5년 이하 근무, 2=6~10년 근무, 3=11~15년 근무, 4=16~20년 근무, 5=21~35년 근무, 6=36년 이상 근무
분석을 위해 다음과 같이 가설을 세웠다.
H1 : 연령[agecat]에 따라 받는 시간당 급여[wage]에는 차이가 있을 것이다.
이 가설을 검증하려면 ‘일원배치분산분석(one-way ANOVA)’을 해야 한다. 순서는 다음과 같다. [분석 → 평균 비교(M) → 일원배치 분산분석(O)]
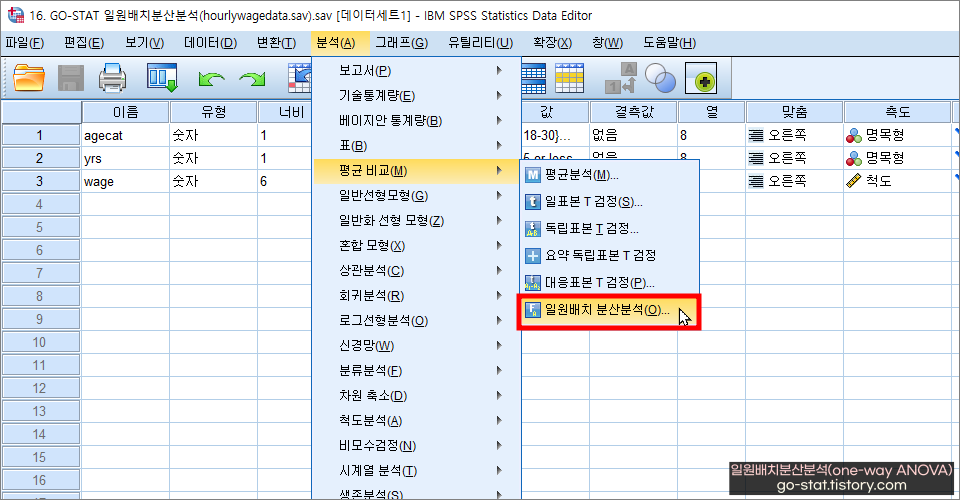
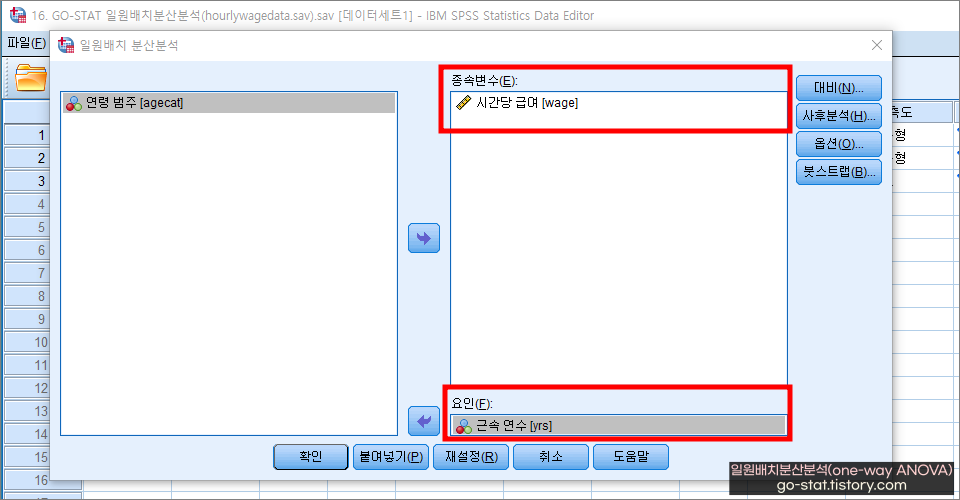
독립변수에 해당하는 ‘연령[agecat]’ 변수를 ‘요인(F)’ 칸에 넣어주고, 종속변수에 해당하는 ‘시간당 급여[wage]’를 ‘종속변수(E)’ 칸에 넣어준다. 중요한 건, ‘요인(F)’에 들어가는 변수는 3개 이상의 집단으로 구성된 범주형 자료여야 한다. 반면, ‘종속변수(E)’ 칸에는 등간 또는 비율 척도로 구성된 연속형 자료 변수를 넣어주면 된다.

‘확인’을 누르기 전에 일원배치분산분석(one-way ANOVA)에서는 몇 가지 체크해야 할 옵션이 있다. 먼저, ‘대비(N)’는 크게 건드릴 부분이 없다. 반면, ‘사후분석(H)’은 거의 반드시 체크하는 편이다. 사후분석 옵션을 체크하면 그에 따른 결과를 확인할 수 있기 때문이다. 사후분석은 쉽게 말해 이런 것이다. 분산분석만 진행할 시 단순하게 결과의 유의성만 알 수 있다. 즉, 3개 이상 집단 간의 평균의 차이가 유의한 지 or 유의하지 않은지만 알 수 있는데, 사후분석(또는 ‘사후검정’이라고 함)을 진행하게 되면 어떤 집단이 통계적으로 높고 낮은 지 비교할 수 있는 것이다. 비교하는 방법은 아래의 포스팅에서 자세히 설명하였다.
‘사후분석(H)’은 크게 ① 등분산을 가정함과 ② 등분산을 가정하지 않을 경우에 따라 선택할 수 있는 항목이 다른데, 내가 가진 자료가 ‘등분산을 가정함’에 충족하는지 위배되는지 알기 어렵다면 일단 ‘사후분석(H)’은 빈칸으로 남겨두고 ‘옵션(O)’에 들어가 준다.
‘옵션(O)’에서 ☑ 기술통계(D)와 ☑분산 동질성 검정(H)에 체크하고 ‘계속’을 누른다. 이어서 ‘확인’을 누르면 분석 결과창이 표시된다.
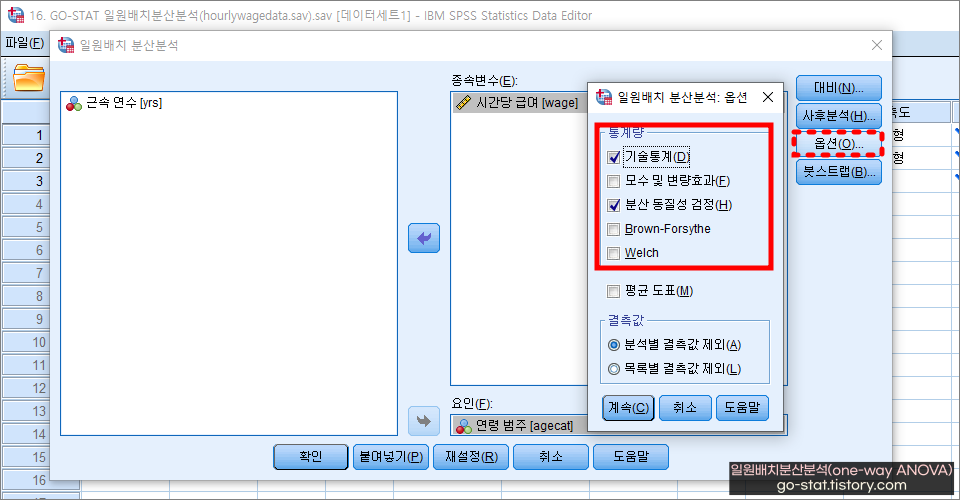
먼저 ‘기술통계’ 표에서 ⓐ 부분을 보자. ⓐ 부분에는 연령[agecat] 별로 표본의 수(N), 평균, 표준편차, 최소/최댓값이 나와있다. 연령은 총 세 범주로 구분되어 있는데, 각각의 샘플 수가 ‘1=18~30세(n=468명)’, ‘2=31~45세(n=1,582명)’, ‘3=46~65세(n=861명)’으로 범주마다 샘플의 수가 동일하지 않았다. 이 부분을 왜 언급했냐 하면 샘플(표본)의 수가 동일할 때 사용할 수 있는 사후분석이 있고 샘플의 수가 동일하지 않아도 사용할 수 있는 사후분석이 있기 때문이다. 일단, 이 정도까지만 알고 다음으로 넘어가자.
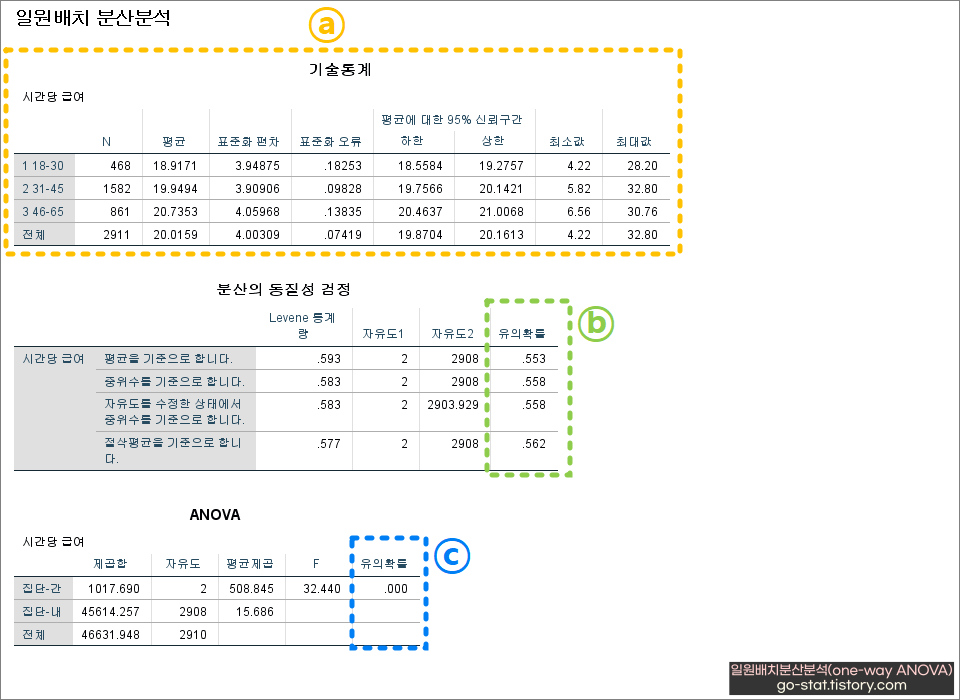
- ▶분산의 동질성 검정 결과, 유의확률 (p값) > 0.05 일 때 분산의 동질성이 만족됨
- ▶ANOVA 결과, 유의확률 (p값) < 0.05 일 때 집단 간 차이가 유의하다고 해석
사실 중요한 건 ⓑ 부분이다. 분산의 동질성이 만족된 상태에서 일원배치분산분석(one-way ANOVA)의 유의성을 보는 것이 정확하기 때문이다. 분산의 동질성이 만족된 상태라 함은 ⓑ p>0.05일 때를 의미한다. 즉, 분산의 동질성 검정에서 p값(유의확률로 표시된 부분)이 0.05보다 크면(p>0.05) 분산의 동질성이 만족된다는 의미이고, 반대로 분산의 동질성 검정에서 p값(유의확률로 표시된 부분)이 0.05보다 작으면(p <0.05) 분산이 동질성이 위배된다는 뜻이다. 이해가 잘 되지 않을 수 있지만 분산의 동질성 검정 결과로 p(유의확률)값이 0.05가 넘을 때 결과해석에 유리하다는 것을 기억하면 된다.
ⓑ 부분이 p>0.05로 나타났다면, 이어서 ⓒ 부분을 보면 된다. 이 부분은 일원배치분산분석(one-way ANOVA) 결과의 유의성을 단번에 알 수 있는 부분이다. 여기서는 p(유의확률로 표시된 부분) 값이 0.000인데, 이는 실제로 0이 아니라 0에 수렴할 정도로 작은 숫자이기 때문에 이와 같이 표시되는 것이다. 어쨓든 p< 0.05 이므로 분산결과가 유의한 것으로 나타났다. 즉, ⓒ 부분을 해석하면 연령[agecat]에 따라 받는 시간당 급여[wage]에는 차이가 있다는 것을 의미한다.

H1 : 연령[agecat]에 따라 받는 시간당 급여[wage]에는 차이가 있을 것이다. → 채택(o)
여기까지 따라왔다면 가설의 채택 여부를 알기에는 어렵지 않았을 것이다. 하지만, 일원배치분산분석(one-way ANOVA)의 단점은 어떤 독립변수의 범주 평균이 더 높고 낮은지 대소 비교를 할 수 없다는 것에 있다. 이를 보완하려면 사후분석을 진행해야 한다. 조금 전에 열었던 분석 창에서 ‘사후분석(H)’을 추가로 눌러보자.
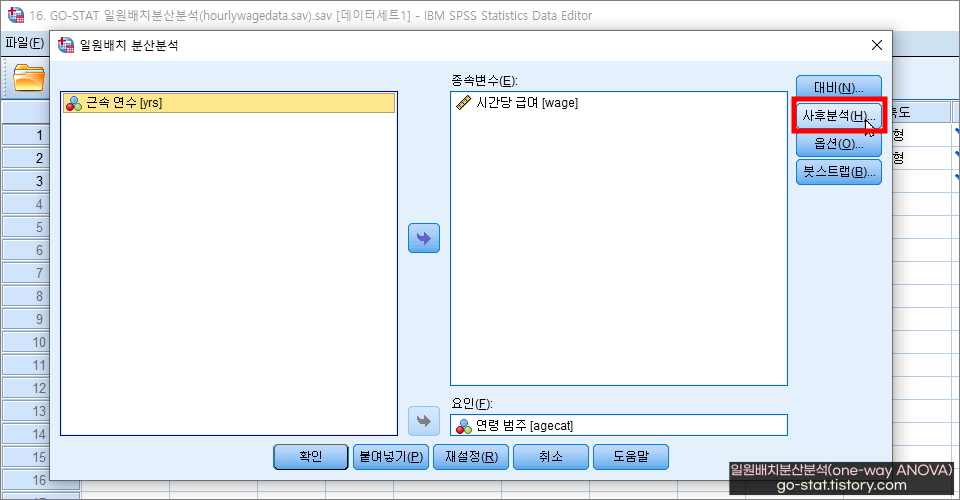
참고로 나는 등분산을 가정하고 표본(샘플)의 수가 동일하지 않은 경우에 사용할 수 있는 ‘Scheffe’ 방법을 통해 사후분석을 진행했다.

사후검정에 대한 결과는 아래에서 확인할 수 있다.
※ 분산분석에서 선택할 수 있는 사후분석의 특징은 이 페이지 하단에 자세하게 정리했다.

① 18-30세, ② 31-45세, ③ 46-65세 간의 [wage] 시간당 급여 수준을 비교한 결과는 다음과 같다. 노란색으로 표시한 부분을 보면 총 3개의 그룹으로 나뉜 것을 알 수 있으며, 각각 시간당 급여가 ① 18-30세($18.9171), ② 31-45세($19.9494), ③ 46-65세($20.7353)로 나타났다. 연령이 높은 그룹일수록 시간당 급여 또한 높았으며, 그 차이가 통계적으로 유의하였다(F=32.440, p< 0.05). 분산분석 결과에 의거하여 평균의 차이를 대소관계로 표현하면 ‘18-30세($18.9171) < 31-45세($19.9494)<46-65세($20.7353)’로 나타낼 수 있다.
Q. 그러면, 근속연수에 따라서 시간당 급여에도 차이가 있지 않을까? 이를 검정하기 위해 다음과 같은 가설을 세웠다.
H2 : 근속 연수[yrs]에 따라 받는 시간당 급여[wage]에는 차이가 있을 것이다.
일원배치분산분석(one-way ANOVA)의 순서는 조금 전 진행했던 방식과 동일하다. [분석 → 평균 비교(M) → 일원배치 분산분석(O)]

‘근속 연수[yrs]’ 를 ‘요인(F)’ 칸에 넣어주고, 종속변수에 해당하는 ‘시간당 급여[wage]’를 ‘종속변수(E)’ 칸에 넣어주었다. 아까와 동일하게 ‘대비(N)’는 건드리지 않고, ‘사후분석(H)’은 ☑ Scheffe를, ‘옵션(O)’에서 ☑ 기술통계(D)와 ☑분산 동질성 검정(H)에 체크했으면 ‘계속’을 눌러준다. 이어서 ‘확인’을 누르면 분석 결과를 확인할 수 있다.
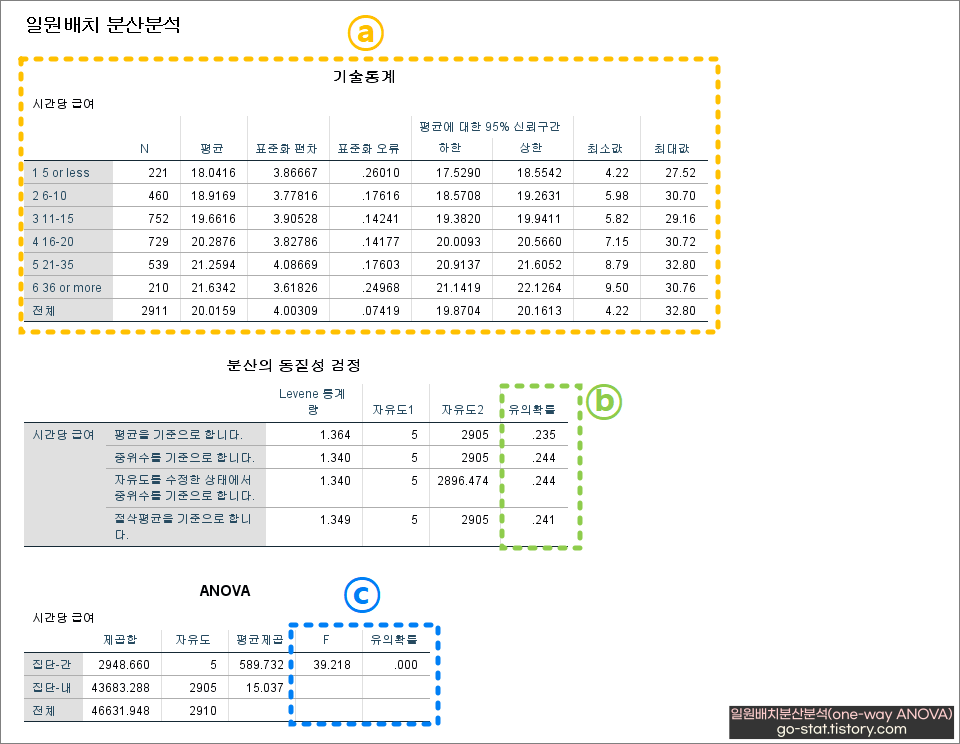
ⓐ 부분에서 근속 연수[yrs] 별로 표본의 수(N), 평균, 표준편차, 최소/최댓값 등에 대한 기술통계치를 확인할 수 있다.
ⓑ 부분에서는 눈을 잘 뜨고 분산의 동질성이 충족되었는지 점검해야 한다. 이 부분을 제대로 점검하지 않고 분산분석에 대한 결과만 제시하는 연구도 있지만 사실 바람직한 방법이 아니다. 언급한 대로 분산의 동질성이 충족된 상태는 ⓑ p>0.05일 때를 의미한다. 이 경우 평균을 기준으로 분산의 동질성을 검정한 결과, p값이 0.235로 0.05 보다 크므로 분산의 동질성이 충족되었다.
★기억하자!
분산의 동질성 검정에서 p값(유의확률로 표시된 부분)이 0.05보다 크면(p>0.05) 분산이 동질성을 만족한다는 의미이고,
반대로 분산의 동질성 검정에서 p값(유의확률로 표시된 부분)이 0.05보다 작으면(p <0.05) 분산이 동질성이 위배된다는 뜻이다.
분산의 동질성이 충족되었으므로 ⓒ 부분을 바로 해석해도 된다. 이 부분은 일원배치분산분석(one-way ANOVA)의 결과의 유의성을 알 수 있는 부분이다. 여기서는 p(유의확률로 표시된 부분) 값이 0.000(실제로는 0이 아니라 0에 수렴할 정도로 작은 숫자이기 때문에 이와 같이 표시됨)이므로 0.05 미만이어서 유의한 결과가 도출되었다. 즉, ⓒ 부분을 해석하면 근속 연수[yrs]에 따라 받는 시간당 급여[wage]에 차이가 있다는 것을 의미한다.

H2 : 근속 연수[yrs]에 따라 받는 시간당 급여[wage]에는 차이가 있을 것이다. → 채택(o)
이어서 사후검정에 대한 결과를 알아보았다. 분산분석은 세 개 이상 집단의 평균의 차이가 유의한 지 검증하는 분석 방법이라고 소개했다. 그렇다면, 분산분석이 유의하다고 나왔을 때 어떤 집단의 평균이 높고 낮은지 알고 싶다면(대소비교를 하고 싶을 경우) 사후분석을 진행해야 한다. 초록색 점선 부분을 보면, 1집단의 시간당 급여가 4집단의 시간당 급여보다 낮은 것을 알 수 있다. 반대로 말하면, 4집단에 속한 근무자(21년~35년, 36년 이상 근무)의 급여가 1집단에 속한 근무자(5년 이하) 보다 높다는 것을 의미한다. 1집단에는 6~10년 근무자도 포함되어 있으나, 6~10년 근무자는 1과 2집단에 모두 걸쳐 있으므로 비교하기에 애매한 부분이 없지 않아 존재한다.

개인적으로는 사후검정이 분산분석 이후에 꼭 진행되어야 하는 분석방법이라고는 생각하나, 포스팅을 하면서 사후검정 결과에 관하여는 자세히 해석하지 않았다. 그 이유는 어떤 사후분석 방법을 택하느냐에 따라 그 결과가 달라질 수 있기 때문이다.
분산분석 그 자체의 결과는 동일하겠지만, 대소를 비교함에 있어서 사후분석 기법마다 그 결과에 차이를 보인다는 뜻이다. 그래서 어떤 논문에는 조금 더 설득력 있는 결과를 제시하기 위함인지(..?) 2개 이상의 사후분석 결과를 제시한 경우도 더러 있다. 아무쪼록 사후검정을 통해 대소간의 비교 결과를 제시할 줄 안다면 분산분석 결과만을 제시했을 때보다 적을 수 있는 시사점이 풍부해진다. 참고로 분산의 동질성이 충족되지 않았을 때(p>0.05) 사용할 수 있는 사후분석 기법도 있으니 참고해 보길 바란다.
분산이 동일한 경우에 사용할 수 있는 사후분석 방법:
▶ LSD :
- 비교 대상의 표본의 수가 동일하지 않아도 사용 가능한 방법
- 오차의 비율을 통제하지 않아 상대적으로 엄격하지 않은 기준이 적용되는 기법
▶ S-N-K(Student-Newman-Keuls)
- 비교 대상의 표본수가 동일한 경우에 사용
- Tukey와 유사하지만 임계치가 다르고 기각 값에 차이가 있다는 특징을 보임
- 대체로 Tukey 보다는 검정력이 우수하다고 알려져있으며, S-N-K 방식은 모든 단계에서 실험 전체의 유의 수준을 적용하고 있음
▶ Waller-Duncan :
- t-검정에 기반한 다중비교 방법으로 베이지안원리에 따라 제1종 오류와 제2종 오류율을 비교하고자 할 때 사용됨
▶ Bonferroni :
- 분산이 동일하되 비교 대상의 표본의 수가 동일하지 않아도 사용 가능한 기법
- 각각의 귀무가설에서 유의 수준을 수준의 개수로 나누는 방식으로 Tukey보다는 엄격하고, Scheffe보다 관대하다고 알려진 사후검정 방법
- 모수 또는 비모수 통계에 상관없이 응용 범위가 넓은 것이 특징이나, 비교대상이 늘어날수록 검정력이 약해질 수 있음
▶ Tukey
- 분산이 동일하고 비교 대상의 표본수가 동일한 경우에 사용
- 모든 집단 조합에 대하여 분석 가능하여 적용분야가 넓으나 표본의 수가 적으면 정확도가 함께 떨어짐
▶ Sidak:
- 비교 대상의 표본의 수가 동일하지 않아도 사용 가능한 기법
- Sidak의 특징은 가능한 모든 집단에 대해서 조합을 만들며 그 조합을 분석하고 이에 관한 쌍대비교 결과를 제공하는 것이 특징임
▶ Tukey의 b :
- 스튜던트화 범위 분포를 사용하여 그룹 간의 쌍대비교를 수행하는 방식으로 사후검정이 이루어짐
- Tukey 방식의 검정력은 S-N-K보다 떨어진다고 알려져 있으나 1종 오류 통제에 있어서는 오히려 효과적이며, Tukey와 S-N-K의 통계량을 평균내어 사용함
▶ Dunnett :
- 한 개의 대조군을 설정하고 여러 실험군과 비교하는 분석에 사용될 수 있는 사후분석 기법.
- 이는 하나의 집단을 기준으로 다른 집단들과의 차이 분석을 하고자 할 때 적합하지만 모든 집단 조합을 대상으로 검정하지는 않음
▶ Scheffe:
- 비교 대상의 표본 수가 동일하지 않아도 사용 가능한 기법(이번에 사용한 방법)
- Scheffe는 F-분포에 기반하여 각 그룹들 간의 평균 값에 대하여 발생 가능한 짝들을 놓고 비교를 동시에 진행하는 방법임
- 따라서 Scheffe는 불균형 자료 속에서도 단순하고 복합적인 평균 비교가 가능하며, 보수적이고 엄격한 방식을 적용하고 싶을 때 사용됨
▶ Duncan :
- 분산이 동일하고 비교 대상의 표본 수가 동일한 경우에 사용하는 기법
- Duncan은 집단을 분리하려는 성격이 매우 강하기 때문에 집단을 면밀히 나누어 비교하고 싶을 때 사용될 수 있음
▶ R-E-G-W의 F(Ryan-Einot-Gabriel-Welsch) :
- 비교 대상의 표본수가 동일한 경우에 사용하며, F 검정을 기준으로 하는 다중 단계감소 방법중 하나임
▶ R-E-G-W의 Q :
- 비교 대상의 표본수가 동일한 경우에 사용하며, 스튜던트화 범위를 기준으로 하는 다중 단계감소 방법임.
▶ Hochberg의 GT2 :
- 비교 대상의 표본의 수가 동일하지 않아도 사용 가능한 것이 특징이며, 스튜던트화 최대 계수를 사용하는 다중 비교 및 범위 검정 방법으로 Tukey의 정직 유의차 검정과 유사함
▶ Gabriel :
- 비교 대상의 표본의 수가 동일하지 않아도 사용 가능하며, Hochberg의 GT2보다 효과적으로 쌍대비교를 수행하는 방식으로 사후검정이 진행됨
분산이 동일하지 않은 경우(등분산을 가정하지 않음)에 사용할 수 있는 사후분석 방법:
▶ Tamhane의 T2 :
- Games-Howell보다 엄격한 다중비교 방법을 제공하며, 제1종 오류 통제에는 조금 더 보수적인 결과를 제공함
▶ Dunnett의 T3 :
- 집단별 표본의 수가 동일할 때 사용하며, 집단별표본의 수가 50개 미만일 때에는 Games-Howell보다 대체로 검정력이 우수하고, 집단별 표본의 수가 50개 이상일 때는 Games-Howell보다 제1종 오류가 높아지는 경향이 있음
▶ Games-Howell :
- Tukey의 사후분석 방법을 개선하기 위해 고안된 방법으로, Welch 방식의 자유도 기법을 응용한 형태의 사후분석 기법임
- 이는 집단의 표본수가 달라도 사용 가능하나 표본이 6개 미만일 때 제1종 오류의 확률이 높아짐
▶ Dunnett의 C :
- 집단의 분산 동질성이 충족되지 않았을 때 사용하는 건 마찬가지이나, 스튜던트화 범위를 기준으로 쌍대비교를 할 때 사용함